My students arrived and the Estimation 180 warm-up (or "Do Now" as we are calling it this year) as usual. I gave them 3 minutes where I was walking around with the stamp to make sure they had it done. I told them if it wasn't stamped in the first 3 minutes, it wasn't going to be. I spend WAY too much time warming the class up at the start of class.
They are getting better at the Collins 1 writing that I'm asking of them. Write 2 lines of explanation, get a stamp! They love those stamps!
We did a brief review of the topics that they should have been working on, answering any questions that they had. Then, while they continued to work independently, at their own pace, I walked around, working with small groups and individuals, helping to clarify concepts and checking off completed work.
Halfway through the period, they took their break. Instead of "Alright! Get back to work!" when they returned, I facilitated a 5-10 minute discussion on scientific notation, the next topic that we will be covering.
In the first class, I made this mistake (good choice) to ask how far away they thought the sun was from the Earth. The purpose was to talk about the benefits of using scientific notation for very large and very small numbers.
Instead, we had a 20 minute conversation about gravity, the speed of light and a few other physics concepts.
They displayed curiosity and were asking questions faster than could answer them. I need to find a way to get them to realize that curiosity and use it to explore their interests.
I want the geometry students doing more critical thinking, so I started looking for a good problem that they could do in their groups. I wanted to find something that related to the content we have been covering, so I starting poking around Five Triangles. Since we haven't talked about circles and aren't really talking much about triangles yet, I searched for something related to parallel lines. What I found was this:
I asked the students to find the measure of angle A, justifying all of their steps and then present those to the class. Of the 6 groups, they were all on the right track, but most were making assumptions that sent them in the wrong direction. The ideas were great and varied, but the justification was lacking. We talked a ton about mak9ing assumptions and being able to back up their claims. We will work on it.
Regardless, I was very pleased with the group work and the persistence.
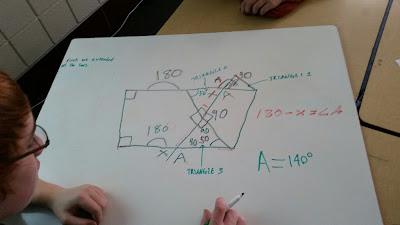
I absolutely love that problem. For high flyers, you can have them figure it out for x instead of 50. #180 is a similar "feel" and also requires fairly little geom knowledge (just isosceles triangles & circle radii), though some may need a hint about what line to add.
ReplyDelete