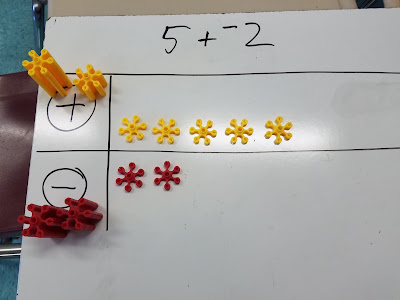Day 27: Reassessments

After a week of students looking at their skill scores and practicing various problems, today was reassessment.  Any student who earned less than 4 on a skill on the quiz last week was able to reassess that skill, if they chose to.

I went around the room, asking who wished to reassess which skill and handed out the papers accordingly.

In one class, the scores all came up and I was incredibly impressed.  In another, every reassessment score was either the same as previous demonstrated, or lower.

I will be interested to see what happens with the rest of the classes.  I won't be doing reassessments every week.  After speaking with some other teachers, I've decided it will probably be two more times by the end of the marking period and maybe once every three weeks after that.

I'm ready to move on.  I need to make a conscious effort to spiral back and cover the material that many of the kids still need to work on.

Yesterday, I presented to the faculty of the whole district about what I'm doing with the Standards-Based Grading and reassessments.  I feel as though I rambled a bit, but several other faculty members told me that they enjoyed it and would like to speak to me about it further.

This week has been odd, with assemblies, fire drills, meetings and trainings.  I'm tired.

I'm thankful that I was able to spend some quality time with my department today. I am working with a truly fantastic faculty.

I wish you all a great weekend!

Day 26: A Lunchtime Anecdote

The following conversation was relayed by a colleague of mine, having overheard it in her class.

"Mr. Aion doesn't teach!"
"He TOTALLY does! He just doesn't teach like other teachers.  He makes you think for yourself."
"Yeah, but I don't want to think!"


I think this is what I want.  I don't want students talking about me as much as talking about education.  I want my students thinking about the best way to learn.  I know that my teaching style and the fact that I lean heavily on inquiry-based lessons and these are VERY much outside of the experience of most students and parents.

"You're supposed to be teaching us" is often code for "you're supposed to be standing in front of the room and lecturing."  Education research clearly demonstrates that lectures are not the most effective form of knowledge acquisition.  Lecture does well enough if your goal is to know facts, but that's not my goal.  I want my students to have skills and to be able to think.

I want my students to be able to think.

The biggest complaint that teachers get when they are working through a new type of pedagogy is "he's/she's not teaching us."

Another interesting aspect of this is how students are trained to think about the call and response nature of education.  They think they know what I'm going to ask before I ask it.  They are almost always wrong.  This is leading to some extensive frustration from me as I have to repeatedly say "Stop. Listen to the question I'm asking."

We have been talking about the language of multiplication and division in Math 7.  I've been working with framing multiplication as "5 times 3 means 3 groups of 5."  This was a deliberate choice so that talking about division can be framed as "15 divided by 3 asks us how many groups of 3 are there in 15."

So I wrote 15 divided by 3 on the board and immediately hands went up.

"Put your hands down, please. I haven't asked my question yet."
**hands go down**
"How..."
"5!!"
"I appreciate your enthusiasm, but that's not what I'm asking.  How would we read this question, using the specific language that we've been talking about?"
"5!!"
"That isn't what I asked. I know that you know the answer. Listen to my question. How do we read this in terms of the language of groups?"
"15 divided by 3 is 5!"

I love that I have some students who understand what I'm doing and are able to explain it to their classmates.  I have great hope that more will come around.

It's a process, for them and for me.

Day 25: "YOU Should Wear It!"

I'm starting to create my reassessment quizzes for my students.  I've never been great at either organization or planning ahead, so this is a new experience for me.  My plan is to have a separate page for each skill so kids can take only what they plan to reassess.

I'm discovering that finding, or writing questions for specific skills can be a bit tricky.  I'm having difficulty with the wording and struggling with how to determine proficiency in several cases.

I don't want to be checking calculation, but rather conceptual understanding, which is tricky.


I'm also not sure what to be doing with my Integrated Math class.  They've been working on statistics and surveys over the last few weeks, but now that chapter is at an end.  Our culminating activity was that students designed, distributed and analyzed their own surveys.  There was an interesting variety of topics and presentations.

One group surveyed the students and asked their opinions and experiences on the school dress code.

The juxtaposition between the last two graphs was, by far, the most interesting to me and not at all surprising.

"Yeah, uniforms are a GREAT idea...for someone else!"

Other topics included video game preference, animal preference and correlation between favorite music and favorite medium of art.


The population of this class is an interesting mix of kids who have not traditionally done well in math and those who have, but didn't want to take Calculus this year...

The next chapter in the book is about properties of real numbers.  The same topic that I'm covering with my 7th graders.  It's WAY too basic a topic for this class, but without a curriculum, I'm not sure what to do.

There's incredible freedom knowing that I can do whatever I want, but it's also pretty terrifying.  I could run it like a genius hour class, but I'm not sure how.  I could use it as a math refresher course, picking interesting topics from the book, but I'm not sure how that would work either.  I'm going to have them do programming for the next week or two until I figure out a more encompassing theme.

I need to figure it out.

Day 24: Vinculum

I think that the low scores on the quiz on Friday, combined with progress reports yesterday and the long conversation about reassessing skills were all strongly correlated with the student's willingness to pay attention today.

In any event, they were very attentive and we had some pretty great discussions.  In Math 7, we started the section on multiplication of integers and framing in terms of repeated addition.  Standard of Mathematical Practice 2 asks students to think about numbers in many ways.  So we did.

We came up with 10 ways to represent multiplication.

I spent the entire period on 2 examples because I wanted to emphasize the language that we will be using going forward.

Being able to think about multiplication as "3 groups of 2" makes the transition to division much easier, especially division of fractions, using phrases such as "How many groups of 1/2 are there in 3?"

In Pre-Algebra, we looked at specific examples from the quiz and talked about the common mistakes that I saw in assessing.  The two major problems with long division were putting the decimal in the wrong place and having the vinculum (the repeater bar) cover either too much, or not enough.

I know fancy words!

When we discussed converting repeating decimals back into fractions, I showed the algebraic method, but we talked more about strategies that we could use to estimate and then find the answer.


It's a process, but I can feel that we're moving in the right direction.  I had a parent contact our superintendent in a fury over what was happening in my class.  After writing directly to the parent, she thanked me for my thoughts and expressed appreciation for my methods.

It was a good day.

I hope to put a vinculum over this feeling.

Day 23: "I Got A 77%!"

Standards-Based Grading is new to my students as well as to me.  After their first SBG quiz on Friday, I spent considerable amount of time putting the data into a nice spreadsheet, adding features and making it easy to understand.

Before I handed the quizzes back today, I went over the sheet and explained what we were looking at.  I asked them to tell me what stood out to them.

This version automatically converts the various skill scores into the 100% scale for easy transfer to our traditional report cards.  It also, through the chart on the side, gives us an easier way to quickly see which skills are weak in all of the sections of a class.

Through trial and error, I discovered that it was better to go over this chart before I gave the quizzes back.

I reminded them that this is merely a snapshot of one moment in time.  Any skill can be reassessed as many times as necessary.  I also expressed my pleasure that no one earned a 4 on every skill.  Everyone has some growing to do and that's fantastic!

Now we have this information. What do we do with it?

Today was #MistakeMonday and I incorporated that into our task.  Instead of having students write about a mistake they made last week, I had them write about their quizzes.

I had them take out a clean piece of paper and make 3 columns.  The first column was labeled "Skill #" with the second labeled "What Kind Of Mistake" and the labeled "Plan for Reassessment."

For each skill, the students were asked to identify whether the mistake they made was a careless error, a conceptual misunderstanding, or something else.  I explained the differences between these by putting the following two equations up on the board:

3+4=8

3+4=34

We had a brief discussion about why each one was wrong and, most likely, why that mistake was made.

In the last column, the student was asked to lay out a plan to improve on the skill before they reassessed.  That plan could include staying for extra help, doing more practice problems, working with friends, watching online videos, etc..

My plan is to offer reassessment on Fridays.  After a student has shown me that they have made an effort to improve their ability, they can reassess whatever skill they want, replacing the old score with the new.  I showed them an example in the spreadsheet of how the new score changes the overall average and leaves no record of the first score.

In one class, I had to field the same questions over and over from students who are used to getting straight A's and were not used to being able to correct their mistakes.

Another reason I love SBG as much as I do is because it allows students to make mistakes with no penalty and encourages them to learn and grow from those mistakes.


So I handed back the quizzes and students were both confused and upset.  On a quiz with 4 skills, there were 4 scores.  One student looked very sad and I asked her what was wrong.

"I got a 77%. That's really bad!"

I looked at her quiz.  Her scores were 3, 3, 3, 1.

This means that she knew what she was doing on 3 of the 4 sections and completed them VERY well.  None of that mattered, however, as she was focused on the 1 and the converted percentage.  I spoke with her about her strengths and celebrating those before focusing on weaknesses.

It didn't seem to sink in.

I know this will take a while, but I think it's worthwhile.

Some of my nerdier colleagues are SUPER excited and keep coming to my room to ogle my spreadsheets. I hope they buy me dinner first.

Day 22: Spreadsheet Geek

As I've stated previously, I'm diving into Standards-Based Grading this year.  Several other teachers in my building have expressed interest in it as well and have asked me to talk to them about my process.

We have a new superintendent.  In the next two months, we will have a new elementary principal and next year, will have a new high school principal.  To me, this appears to be an ideal situation to make some monumental changes.  I spoke with a few of the other teachers and they agreed.

I went to put the bug in my superintendents ear and she was very amenable to the idea and has asked me to speak to the faculty at our meeting next week.  I'm VERY excited.

Since this was the first time that my students had experienced an SBG-style quiz, I put up a few tips for them.

I read over these and emphasized that none of the grades were permanent, as long as they were willing to reassess those skills.

I had lots of pushback from one of my classes, who flew into a panic about not knowing what was on the quiz, that we were even having a quiz, or that the quiz would be graded.  I tried to have patience with them since many in this group are the "accelerated" students and have grade pressure on them.

The harm that we do to our students by making them think they not only have to get everything perfect, but do so the first time, is staggering.

I know this process will take a while, but I believe in it and the research backs it up.  With administrative support and other teachers getting involved, I believe it will be alright.



I am a HUGE nerd for spreadsheets!

I'm not great with making them look all fancy schmancy, but I love adding functionality and color-coding!

Standards-based grading provides such and incredible wealth of information and an excellent opportunity to play around with spreadsheets!  So I made one!

This is the spreadsheet that I'll be presenting to the faculty next week in an effort to sell the idea of
SBG.  So what does all of this stuff mean?

I have taken all of the standards and put them into simple "I can" statements, such as "I can describe situations where opposite quantities combine to make 0. (Standard 7.NS.A.1A)" and given them specific numbers.  That standard is Skill 2.

Each section on the quiz covered a specific standard and students received a score for each.  This quiz covered 6 standards, so it had 6 sections and students earned 6 scores, as listed above.

There are a ton of ways to describe what each number means and I use a Star Wars-based poster, which is fantastic!

It boils down to:

4: WOW! YEAH!!
3: Well done.
2: Almost
1: Yeah...no
0: Not assessed

I used conditional formatting to set up color gradients. 3 and 4 are green, indicating that the student is good to move on. 0, 1 and 2 show some (or lots) of work to do.

Above the skill, I have the sheet add the number of students who have earned each score.  This allows me a quick glance to see which skills need to be readdressed as a group, instead of individually.

For example, the above graph shows me that my students are doing pretty well on Skills 1-4, but that we could still do some work together on Skills 5 and 6.

With individual students, I'm able to look across the row and see what their strengths are and on which skills I should work with them.

One of my favorite aspects of this sheet is the ability to sort. When we are looking at what topics to cover next, I can sort the list by skill score and group together students accordingly, either struggling students together so I can work more closely with them, or heterogeneously so they can help each other.

In terms of Skill 6,  I may have the students with 3's and 4's teach the others in pairs, or I may put all of the 2's and 1's together, work with them myself while giving the rest a different task.

SO MANY POSSIBILITIES!!!


I like data, but most of the student data that we collect is not done in a way that makes it easy to address.  This timely and brilliantly color-coded feedback will allow me to create more data-driven instruction.

I'm pretty pumped.

Now, to spread the good word!

I was a bit distressed, however, at the number of students later in the day who looked at the test and immediately gave up. Several students were crying about how difficult it was and how they were failures and going to fail.

There is a TON of work for me to do in terms of mindset.

Day 21: Tears: A Guest Post

I've been encouraging fellow teachers to write and reflect and have offered to host their voices whenever they would like.

The following post was written by a special education teacher who works with high-risk youth. The names have been changed, but I have made no edits.

I cried today. In front of a room full of Juniors in High School- I cried.

When he walked into my classroom this afternoon, I’d let my heart hope that the Gods of Special Education had found a way to give this young man just one more chance… after all, how many times do we hear him will the pleas? “C’Mon- Miss.… gimmie one more chance?”

How many times do we rebuff them? Scoff a little bit and walk away?

And here I am--- hoping this kid who has terrorized every school he’s been at for the past 6 years will get that mythical “one more chance?” I must be nuts.

He and I had talked about this last week… I’d heard, through the teacher grapevine, that the powers at be were sending him back to the Alternative program… this time with no hope of returning to our building.

I love that program for the reprieve it provides the colleagues I see everyday from the students who just can’t handle a typical school. Those individuals who are overwhelmed by the sheer size and magnitude of our building and decide to make it their playground (rather than their educational haven) get sent to “that place” and become somebody else’s problem.

Joe had been bounced in and out of the Alternative building for the better part of 3 years. He’s probably spent an equal amount of time in the high school and that other place. During his most recent return trip last year, he promised me that he would never go back there. He’d told me he was sick of not being challenged and that he wanted to EARN his diploma. He had goals. He was back on track. I vowed to help keep him on the straight and narrow.

Then his mom died.

At the funeral, he clung to me and told me he’d failed her as a son. In those same breaths he renewed his promises to “make it”- to graduate from the high school and help make his mom’s (and his) dreams come true. We had one year to make it happen.

Over the summer, Joe continued to work at KFC (now using his wages to help support his estranged father who had moved into his mom’s house in an effort to act as a parent for the first time in 17 years). He’d lost so much in a few months, but his drive remained intact- be good. Learn. Graduate.

Be good. Learn. Graduate.

Please understand, Joe has never been innocent- he tolerates little that doesn’t meet his standards of perfection, cannot be talked into doing something he doesn’t want to do, and makes his presence very well known. He will never allow himself to be overlooked and stands up for what he believes in. Joe is a fighter- and a damn good one at that. He’s earned 99% of the negative connotations that come before his name. Hell- he’s proud of them. Most teachers can’t stand him. I’ve heard teachers fight to get him out of their classes. Despite this (ah- let’s be honest- it’s probably because of this), Joe is one of my favorite students.

Be good. Learn. Graduate.

He was provided with an opportunity from the district- early release every day. As long as he successfully completed his core classes- he’d earn the credits to graduate, but, if he only attended a half a day, he’d have less opportunity to get himself into trouble. Getting out early meant he could take on more shifts at work. It was a win/win for everyone.

Be good. Learn. Graduate.

Joe’s plan: Work every shift he could at KFC. Save the money. Go to trade school after graduation. Become an electrician. Make something out of his life.

Be good. Learn. Graduate.

He was on his way until his father invited his daughter into the picture. A daughter whom Joe barely knew and who had believed in all the terrible things she’d heard about her little “brother.”

According to Joe: she thought his job at KFC was trivial. She didn’t care about his plans and decided he would amount to nothing. She had no faith in him and managed to convince their dad that Joe would fail.

Joe began to rebel at school, and, well- earned himself his final, one-way ticket back to the alternative school. A year-long sentence to a building that requires little of its students and lumps those with bad attitudes into the same room as those who will be arrested before long.

He got kicked out a few days ago… we’d had a conversation the day before where Joe bared his soul to me. He told me we’d have one more class together and that I’d better make it good.

He never made it to our last class.

But today, Joe showed up at my door (with a security escort) and I’d thought that maybe, just maybe, we’d found one more chance.

He walked into the middle of my classroom with his arms open wide and pulled me into a hug that he wouldn’t let me out of. When he finally let me breathe, he grabbed me up in another huge hug and told me not to worry about him anymore. That he would be fine. That he wouldn’t let this beat him. That there were other kids I should worry about now. He told me he was sorry.

Before he turned to leave (not even the ghost of a last smile on his face), I threw him the bag of cough drops that I illegally kept in my (just for him). He chuckled, ate one, pocketed the bag, and said, “Bye Ms. Kane.”

His stoic resolve broke my heart. Who WAS this man standing in front of me? Where’s the rebellious teenager who would fight for anything he thought was fair? WHY did he have to deal with this?  We’d failed him. I’d failed him. His sister should be drawn and quartered. His mom would be devastated.

And as my door shut behind him, I wiped mascara-stained cheeks and realized- that I was crying in front of a room full of Juniors.

Day 20: Programming

All of my classes will be having a quiz on Friday, giving them a chance to demonstrate their understanding of the skills before progress reports are due.  With that in mind, and in acknowledgement of the frustrations that many of my students are feeling, I took today as a practice day.

In Math 7, we discussed properties of integers again, specifically in light of applications, such as temperature.  We talked about what it means, numerically, for the temperature to change.  I began to worry about the time I was spending on, what I considered, a very basic concept.

Then I remembered that it's only a basic concept to me and, since I'm now teaching 7th grade, it's a core skill.  I have the opportunity to build a solid base of skills when they are developmentally appropriate, rather than trying to lay a foundation once the house is actually built.

Instead of worrying about all of the topics that I'm supposed to cover, I'm trying to focus on the basics and helping my students to develop better numeracy.  Comfort and confidence with numerical operations will serve them MUCH better as they move forward in math and in life.

In Pre-Algebra, I "involuntarily collaborated" with EngageNY, and found an excellent packet of scaffolded problems and questions that are based in the standard we are covering.  I handed them out, gave my basic directions and said "Go!"

I spent the period circulating through the room, helping students with directed questions, rather than answers.  Kids were using whiteboard, working together, moving around the room and learning where they were comfortable.  I was incredibly pleased with what I saw.

Now, my Integrated Math class...

This class is filled with students who either miss a bunch of school, aren't ready for Statistics, or wanted an easy math course.  Their skills and interests are incredibly varied.  On top of this, I don't really have a curriculum or standards.

The first chapter in the book that is traditionally used covers basic statistics and surveys.  We've been talking about those for the past few weeks.  Their chapter project was to design and distribute surveys on a topic of their choosing, then analyze and display the results for the class.

The next chapter seems to be an odd combination of exponents and volume.

I have freedom with the course and would like to do something else.  I ran this past the students today and they seemed pretty excited about my thoughts.

Why not programming instead?

We have courses in the school that cover HTML and Microsoft Office, but what about something else? Could I get them working on a computer language at their own pace?  I could learn one along with them.

There is an incredible bounty of resources that help people learn programming and computer languages, including Code.org, CodeCademy, CodeCombat, etc.

I ran this idea past another teacher and she thought it was a great idea.  In theory, the kids learn a language of their choice and then produce something cool by the end of the marking period, like a video, basic game, tutorial, etc.

I have more reading to do.  Should I pick a language for them? Should I let them choose? Should the first task be to pick a language based on what they want to do?

Day 19: Keep Your Head Up

Progress reports are due on Friday.  As per my usual routine, I don't have a ton of grades in yet.  My students in Integrated only have 1 and the other classes only have 2.  This means we will be having a quiz on either Thursday or Friday of this week.

THAT means that I need to hit certain concepts under my new Standards-Based Grading system, so that I CAN give a quiz.  In the Math 7, I'm not too worried since what we've done so far has covered that material.  In the Pre-Algebra classes, I have some concerns.

Up to this point, the Pre-Algebra class has been following the Math 7 standards as a review of concepts.  Today, we started working on 8.NS.A.1 (I can show that every number as a decimal.)

I had the kids pick spots on the whiteboards and gave them a few fractions to convert into decimals.  The idea was to have them make conclusions about the types of decimals that can be made from fractions (terminating or repeating) as a lead-in to a discussion of rational numbers.  What was supposed to be a warm-up took the entire class.

There are several issues that I'm finding with foundational understanding, some of which can attributed to summer attrition, but not all.

In my advanced class, we had a conversation about choices and the wisdom behind the concept of "if you are struggling with a concept, it may make sense to pay attention when we go over it."


In 2013, I had the pleasure of meeting Max Ray-Riek.  In the intervening years, I've been able to spend some time with him and had him observe my teaching.  He told a story about being in band and losing his place.  Take a few minutes and watch this:


My students do exactly this.  We have incorporated such shame is being lost, in making mistakes, that students who are unsure of themselves have a tendency to hide.  When hidden, they don't get their needs met.

Adding to this, there are several students who understand the concepts VERY well and are very vocal about it.  Their enthusiasm and energy is excellent, but can inadvertently make those students who struggle feel even worse about their level of understanding.

I know that it's going to take a while to build that culture where they feel ok saying "I don't understand" and "I need help."

I sincerely hope that I'm able to build it before they fall too far behind.

I need to do a better job of giving independent tasks so that I can circulate through the room and give those quiet students more of a chance to ask their questions in a smaller space.




My frustration at lack on conceptual understanding in one class and behavior in another caused me to snap.  I got into an argument with a student in front of the class and his smirk at knowing what he was doing sent me further over the edge.

I tried to teach afterwards but it wasn't happening.  I stopped mid-sentence, walked to the window, took a breath and asked them to sit down.

Then I apologized.  It was a sincere apology for speaking to them the way that I had been.  I expressed understanding at their frustration and explained my own, while acknowledging that my actions were not acceptable.  I asked them to forgive me and asked if it would be alright if we moved on.

We did.

I approached several students afterwards to apologize to them personally for my actions and to ask what they needed from me in order to achieve and learn.

It happens.

While frustrating, today was still a good day and it has given me more insight into what I need to do for my students.

Day 18: #SBG and a #TURD or Two

On Saturday, I walked to our local coffee shop and sat for a few hours doing grading and setting up my classes for Standards-Based Grading.  There are a ton of resources available online for doing this, so I didn't have to start from scratch.  I know it's going to be a rough transition, but I believe in it and it's been long overdue.

Today, I presented it to my Math 7 and Pre-Algebra classes with mixed results.  Understandably, they had many questions, so once the warm-up and #MistakeMonday were finished, I devoted the entire period to going over it.

Up to this point, both Math 7 and Pre-Algebra have been at the same point.  That changes now as they have different standards.  There is a considerable amount of overlap, so we'll be able to use the same resources, but the kids will be at different points.

I think many of the Pre-Algebra kids are going to feel a bit overwhelmed for a little bit, and that's alright.  With the ability to do re-assessments, they will (hopefully) be able to see how to focus their efforts on their weaknesses while celebrating their strengths.

I expect there will be growing pains, both for the students and myself.


In the Integrated Math class, we've been talking about data analysis and survey design.  Admittedly, I'm terrible at latter, so I'm learning with them.  Today's discussion was being able to identify what is right/wrong with charts and graphs.

I took inspiration from Christopher Danielson and the TURDs (Truly Unfortunate Representations of Data).

I put a series of images on the board and we talked about them.

"What do you notice about these images? What do you wonder about them?"

After the first few, they began talk about scale and survey respondents.  "When they talk about welfare recipients, do they mean children and the disabled? Do they mean retirees? Those people wouldn't hold full time jobs.  What about people who hold full time jobs but still need welfare?"

"Obamacare must be a failure! They only hit 1/3 of their goal!"

"There are 5 times the number of people unemployed than have full time jobs!"

"Nah! Those dates were randomly chosen..."

"No one needs the whole graph!"

What about some controversial topics?

"Twice as many white people are killed by the cops!"

"See? Two years in a row!"

**crickets**

OOPS!!  Did I accidentally bring up social justice? Sorry about that!

#SorryNotSorry

Day 17: Desmos!

If you don't know Michael Fenton and the amazing work that he is doing with and for students and teachers, you are seriously missing out.  I have had the pleasure of spending time with him on multiple occasions and have always left enriched and challenged to improve.

My deep concern over the discomfort and confusion that my students exhibited around negative integers and using counters has sent me on a search for resources.  Yesterday, I had my students use #VNPS (vertical non-permanent surfaces, or "whiteboards") to display their thinking and convey their reasoning to others.

It went off with mixed results.  I am determined to use the whiteboards more often and will be incorporating #VNPS into my class on a regular basis.

Today, however, I had access the computer lab and wanted to try something else, which brings me back to Michael.

He is on the teaching faculty at Desmos, the online graphing calculator that is changing the face of mathematical educational technology.

He is also the designer of multiple activities, one of which I used today!

What I LOVE about it is that from the teacher dashboard, I'm able to see what they are doing in real-time.  I can tell a student to go back and check a certain problem or add more explanation to their answer.

I'm always interested in how some kids will talk on and on, verbally explaining their answers in novel-length expository monologues, but will only type 2-3 broken words if asked to write it down.

At the same time, there are many students who when asked to verbally explain will simply shrug their shoulders.  If, however, you put a keyboard in front of them and ask them to write out what they are thinking, they have no problem going into incredible detail.

If there is any better argument for differentiation of assessments, I don't know what it is.



At the end of the activity, I handed back the quizzes from Wednesday.  The mean class scores for the five sections, out of 19 possible points, were 8, 10, 11, 13, and 14.

"I got a 10?? Out of 19?? I failed!!!"
"Not at all. You got 10 correct. That's a very solid foundation on which we can build! Look at the test and figure out which ones gave you difficulty and why so that we can work together to ensure that you understand the material and can demonstrate that understanding."
"I FAILED!!"
"Again, it means you have room to grow. If you're so upset by this score, then use this experience as something from which to learn. The studying strategies, or paying-attention-in-class strategies that you've been using may not be the best.
"I'm terrible at math!!"
"I'm sorry you feel that way, but I don't. Let's fix the way you see it!"
"I FAILED!!!!"

And so on and so forth...

It's a process.

Day 16: Slow It Down

Addition and subtraction is as fundamental to mathematics as reading is to life.  If a student isn't able to master these concepts and be comfortable using them, they fall further and further behind until the task of catching them up is insurmountable.

I also realized yesterday that I haven't really given them enough opportunity for practice, so that's what we did today.

I had the students scatter around the room and claim a section of the white board as their own.

"Your mission, should you choose to accept it, or not, is to simplify the expression that I put on the board.  In addition, you must also show HOW you obtained the simplification.  You can use counters, a number line, or whatever you want, as long as you show what you did."

The goal of this was to show how, if used properly, the same strategies could be used regardless of the complexity of the problem.  I started with a basic addition problem.


3 + 5

Students who used the number line were able to explain pretty clearly what they did: "It says that we start at 3, so I started there.  Since it's addition, I went up (or to the right) by 5 spaces and ended up at 8."

Those who used the counters were similarly clear: "I started with 3 positive counters since it says 3.  Then I put 5 more positive counters on that since there were no zero pairs, I had 8 positive counters total."

I wanted to see if they could use those same tactics with subtraction.


4 - 7

They did well with this one too, with 95% able to get the correct answer and be able to explain how.

Then it got tricky.  Subtraction is tough, but manipulation of negatives is even more difficult.


5 + -3

For the most part, the kids who were using the number line did well with this one.  They knew that, even though it was addition, by having the 3 be negative, they were going to move down on the line.

The kids using the counters did just as well, knowing that they needed to add negative counters.

Throughout all of this, only 1 student stared blankly at the board, refusing to write anything and claiming "I'm just confused."

This student couldn't explain which part of addition was confusing and continued to refuse to even attempt it.  I'm going to have to have a further conversation.

One other student looked genuinely confused and seemed to have difficulty with the most basic operations, beginning with addition.

Other than those two, things went really well!

Then, when I apparently forgot to knock on wood, things started to fall apart.


2 - (-4)

This was tremendously difficult for a large portion of the students.  They KNEW that the answer was 6, but couldn't figure out why or how to explain it.  Both number line kids and counter kids, knowing what the answer was supposed to be, manipulated their tools to get what they wanted, rather than using those tools to find the answer.

We will have to practice more on this.  I don't think that anything we would do this year will be more important than getting them fluent in these basic skills.



In a prolonged discussion at the end of the day, one of my students said that he thinks that the behavior is "to test you, because you're a new teacher."

Day 15: Backwards

I gave my first quiz today in Math 7 and Pre-Algebra.  The event itself and the results have brought me to two conclusions, one on a small scale and one on a large scale.

On the small scale, I see that I need to spend more time on a few key concepts, specifically addition and subtraction of negative integers.  I am very pleased with the lessons that we did using the counters, but I'm not sure that I gave them enough time to actually practice those skills.

The method of integer operations is new to them and a bit different than what they've been taught.  It will take them time to acquire these skills and guided practice is something that I glossed over.  The average score in one of the classes was 10/19.

Rather than being frustrated about the low scores, I need to recognize how difficult it is for students to adapt to my teaching and for me to adapt to their learning styles.  They are trying, but there will be a period of adjustment.



The second conclusion is that the education system in general is horrendously disrespectful to children and the idea of childhood.

Before I handed out the quiz, several of my students (11 and 12 years old) began to panic.  They were worried that they were going to fail.  They were going to get bad grades and not get into college.  One student told me that she set a goal for herself in 1st grade never to get any grade lower than an A.

There are no conditions in which an 11 year old should even be thinking about college, let alone be worried about not getting in.

A 1st grader shouldn't even know what grades ARE!

I will continue to emphasize to my students that I care about knowledge and not about grades.  I will continue to emphasize that my grades are related to the level of knowledge that they can demonstrate instead of effort put forth.  I will continue to emphasize that we seek improvement, not perfection.



I kept promising myself that I would move to Standards Based Grading and I kept falling down on that promise.  Perhaps this will finally get me off my butt to do it.

Grades are supposed to be indicators of learning.  If a student is worried about grades, it should only be due to their concern about knowledge that they have yet to master.

Grades are the means to an end with that end being knowledge acquisition.

Grades should never be the end.


Now, if you'll excuse me, my unicorn is double parked and I don't want it towed before I head home to Fantasia!

Day 14: Schrödinger's Lesson

Multiverse theory posits that every decision that is made fractures the universe into one where the choice was made and one where it wasn't.  When my alarm goes off in the morning, I must make the choice to get out of bed, or to stay comfy and warm.  The instant when I make that decision, reality splits into two universes, one in which I stay in bed and one in which I go to work.

The universes that are created by this fracturing run parallel to each other.  The closer universes to our own look almost identical because the choices made to create them were insignificant in terms of their impact.  The universe in which I choose the pair of socks on the left is almost identical to the one where I choose the socks on the right.

As you move through the multiverses, further from our own, the choices that changed them become more and more significant, leading them to be drastically different.  The universe where Booth decided not to kill Lincoln is far away.  The universe where Constantine decided not to convert to Christianity is further still.

When you move far enough from our own universe, the decisions made have forged reality into something completely unrecognizable.

Multiverse theory has been explored in countless science fiction novels and short stories, but none so well as The Long Earth by Terry Pratchett and Steven Baxter and Number of the Beast by Robert Heinlein.

In a way, teachers get to experience multiverse theory on a regular basis, especially those of us who teach multiple sections of the same course.

No two classes are exactly the same and, since teachers are not recording devices, no two lessons are delivered in exactly the same way.

In preparation for the quiz tomorrow, I talked about the idea of addition and subtraction as opposite operations in 5 classes.  Each one went differently and enough so that I was concerned I had jumped into an alternate universe.


There is no way that you can script a lesson.  The most you can do is design an experience and adapt as the changes come down the line.

Day 13: There It Is

Having been floating on Cloud 9 for the last two weeks, I'm starting to see the ground again.  I need to reestablish my expectations in class in terms of behavior and respect for the educational environment.

My task is to determine what behavior is age-appropriate and what needs to be corrected.  There are certain aspects that are clear to me, such as interrupting, name-calling and other things that shouldn't be done in polite society.

There is, however, a whole new class of behaviors that I haven't dealt with before and I suspect they are age-based.  These include fidgeting, noise-making and a whole host of childish pranks.

"Who stole my pencil??"
**giggle**


In previous years, when my 14-year olds and up exhibited these behaviors, it was a simple task to point it out to them.  Even though they are still kids, it's often easy to forget how old they are and if reminded that they are almost adults, they will change their actions.

"What are you doing right now?"
"...acting like a child.  Sorry."

With 12-year olds, however, it's very clear that they ARE children.  While they have moments of clarity and maturity, it's impossible to forget how old they are.  They look like children.

In addition to this, the variation in ages and maturity levels plays so differently in each group of students.  Only 13 days in and all of my classes are now in different places.  The classes that are slowing down are still asking great questions and are not falling behind from lack of effort, but simply through differences in understanding.

So now that the sparkly shine (So shiny! So chrome!) no longer looks like perfection, it's time to get down to the hard work of teaching.  I think this is going to be a very good year.

Day 12: Yup!

Today was a day.  I woke up and went to work.

My students finished their diagnostic tests and we had a pep rally.  It was hot in the gym and there are more cheerleaders than football players.

I spent a considerable amount of time wandering my classroom.




I had 2 great posts this week! I'm entitled to a non-post day.

Day 11: HexaCounters

Over the years, I've noticed certain difficulties that seem to be universal among students.  There are certain concepts that are particularly difficult for them to grasp, many of which are basic ideas of numeracy and number manipulation.  This lack of understanding has a tendency to fester over years and make students think that math is some sort of magical subject that works just because that's how it works.  Two prime examples of this are manipulation of positive and negative numbers and almost anything dealing with fractions.

This is a huge problem for students and for society in general and one that I believe can be solved by better teaching.  In many cases, these topics are seen as painful and hard and teachers gloss over them.  We give students formulas or mnemonic devices to remember what to do (flip-change-change or two negatives make a positive) that get them through the test but don't offer deep numerical understanding and lead to problems later on when we cover more complex manipulations.

Since it's the beginning of Math 7 and Pre-Algebra, we are currently examining integer operations.  Conversations with other educators, as well as my own experiences have moved me towards the idea of using counters and manipulative tools to illustrate the concepts of addition and subtraction of positive and negative integers.

Thankfully, I happen to have a giant bin of multicolored interlocking hexagonal blocks that I can have my students utilize for the benefit of their kinesthetic mathematical understanding.

So counters:

"I'm taking us on a field trip, to an actual field.  In this field, I want to make piles of dirt.  If I make a pile, and I didn't bring any dirt with me, what else am I going to have to make?"

"Holes?"

"Exactly! For every pile I make, I have to dig a hole.  At the end of the trip, I push the piles back into the holes. What happens?"

"You're back where you started."

An extended version of this is how we introduce the concept of Zero Pairs, where 1 positive and 1 negative pair together to give us zero.

We started with the basic set-up: a card with a row for positive counters and a row for negative counters.

Before getting into anything complex, we start with addition, to get an understanding of the counters.

We write the expression at the top.

This problem starts with positive 4, so we take 4 yellow counters and put them on our card.

Since this expression is addition, we know that we need to add more counters to our card.  The 3 tells us that we need to add 3 yellow counters.

We now look at the card and count the number of yellow counters, which in this case, is 7.

We did a few examples of this simple problem to get the kids used to moving the counters.  Then we began working with the negative counters.

Again, we write the problem at the top.

Just as before, this problem tells us that we start with 5 positive counters, so we put them on our card.

Again, the addition sign says that we are going to add counters to the card, but this time, we will be adding 2 red counters, because each red counter represents negative 1.

Next, we line up our counters, creating pairs of opposite colors.

Just like with the piles of dirt and the holes in the ground, we can recognize that each pair of red and yellow counters is worth zero.  The positive and negative counters cancel each other out.

With the zero pairs sectioned off, we examine what we have left, which is 3 yellow counters.

What I LOVED about doing this in class was how the students played with the hexagons to use them as they understood.  There were so many ways that they made the zero pairs and the hexagons allowed them the freedom to explore those options.

"First I made them into rows.  Then I stacked them on top of each other.  Anywhere that had the hexagons together, stacked on top, I took them off the row.  What I had left was my answer."

"I also made rows, but I put them together side by side. I pulled off the ones that had pairs."

 

"We started with stacks, so I left them as those stacks. When I put the stacks together, the pairs stayed together while the ones without pairs just spun off the top."

This method was, by far, my favorite!



To give them a chance to see if their methods worked, we did another problem.

Those were just addition problems. Do these methods work with subtraction as well?  We tried one!

We wrote the problem at the top of the card.

Since the problem began with 5 yellow counters, we put them on the card.

Just as the addition symbol told us that we would be putting more counters on the card, the subtraction symbol tells us that we would be taking some away.  The "-2" tells us that we need to take 2 positive counters away.

When we take those 2 counters away, we are left with 3 yellow counters, giving us an answer of positive 3.

"But Mr. Aion, what if you don't have enough counters to take away?"
I'm so glad you asked! Let's try an example of that!

Again, we start by putting 2 yellow counters on our card.

Uh oh! We're supposed to take 5 yellow counters away, but we don't have that many! What will we do!

Oh! I have an idea!

Right now, we have 2 on our card.

We already saw that if we put a red and yellow counter together, they have a value of zero.

That means I can add a pair of red and yellow counters to my card and STILL have a value of 2!

If 1 pair of red and yellow counters is worth zero, then 3 pairs would also be worth zero!

That means I can add 3 pairs of counters to my card and still have the value be 2!

Once those pairs are on my card, I can separate them into their positive and negative counters.

Our problem told us that we needed to take 5 positive counters off of the card.  Since we started with only 2 and put on 3 pairs, we now have 5 yellow counters that we can remove.

After we remove the 5 positive counters, we are left with 3 negative counters, giving us a value of -3.

I really enjoyed working with the kids on this lesson and they loved playing with the hexagons.  I was incredibly impressed with how they picked up the concepts and how they developed new ways of demonstrating what was going on.